Домашнее задание 6В

доделать 634, 636, 638,649

Домашнее задание 7В

1. Установите со­от­вет­ствие между гра­фи­ка­ми функ­ций и формулами, ко­то­рые их задают.

1)

2)

3)

4)

2. На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций вида у = kх + b. Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми и зна­ка­ми ко­эф­фи­ци­ен­тов k и b.

1) k < 0, b < 0

2) k > 0, b > 0

3) k < 0, b > 0

4) k > 0, b < 0

3. Мощность ото­пи­те­ля в ав­то­мо­би­ле регулируется до­пол­ни­тель­ным сопротивлением, ко­то­рое можно менять, по­во­ра­чи­вая рукоятку в са­ло­не машины. При этом ме­ня­ет­ся сила тока в элек­три­че­ской цепи элек­тро­дви­га­те­ля – чем мень­ше сопротивление, тем боль­ше сила тока и тем быст­рее вращается мотор отопителя. На ри­сун­ке показана за­ви­си­мость силы тока от ве­ли­чи­ны сопротивления. На оси абс­цисс откладывается со­про­тив­ле­ние (в Омах), на оси ор­ди­нат — сила тока в Амперах. Ток в цепи элек­тро­дви­га­те­ля уменьшился с 8 до 6 Ампер. На сколь­ко Омов при этом уве­ли­чи­лось сопротивление цепи?

4. На ри­сун­ке изоб­ражён гра­фик из­ме­не­ния ат­мо­сфер­но­го дав­ле­ния в го­ро­де Энске за три дня. По го­ри­зон­та­ли ука­за­ны дни не­де­ли и время, по вер­ти­ка­ли — зна­че­ния ат­мо­сфер­но­го дав­ле­ния в мил­ли­мет­рах ртут­но­го стол­ба. Ука­жи­те зна­че­ние ат­мо­сфер­но­го дав­ле­ния (в мм рт. ст.) во втор­ник в 12 часов дня.

Домашнее задание (6В, 7Б и В, 8В)

Так как проблемы не устранены, пишу с телефона, а задания из учебника.

6В: 635, 636, 638

7Б и В: закончить 519, 507, 486 (3, 4) Алексееву и Дерновой еще и 516

8В: 597 (1,4), 598 (1,4)

Задание для (8в)

Тест 18
Задания: все КРОМЕ: 10, 11, 21-26

Задание для 8В

1. Дана окружность с центром в точке O. AB –диаметр, точка C отмечена на окружности,

угол A равен 29⁰ . Найдите угол C и угол B.

2. AB и AC – отрезки касательных, проведенных к окружности радиуса 8 см. Найдите длину OA и AC, если AB = 15 см.

3. Точки A и B делят окружность с центром O на дуги AMB и ACB так, что дуга ACB на 50⁰ меньше дуги AMB. AM – диаметр окружности. Найдите углы AMB, ABM, ACB.

4. Найдите радиус окружности, вписанной в треугольник, и радиус окружности, описанной около треугольника, стороны которого равны 26 см, 30 см и 28 см.

Задания для 6Б

1. Восстановите ребус:
                                          КИС
                                        +КСИ
                                          ИСК
2.Две чашки весят столько же, сколько 14 блюдец. Один кувшин весит столько, сколько одна чашка и одно блюдце. Сколько блюдец уравновесят кувшин?

3. В файле хранятся 2012 единиц и 1957 нулей. Программа читает и файла два произвольных числа, стирает и записывает вместо них их сумму, Программа запускается многократно. В конце концов, в файле остается только одно число. Чему оно равно?

4. Можно ли соединить 9 телефонов между собой попарно так, чтобы каждый был соединен ровно с тремя другими?

Информатика

Задания

Домашнее задание (6, 7 и 8 классы)

6 класс:

Выполните контрольные вопросы и задания к текущему параграфу

7 класс (алгебра):

1. Из за­ко­на все­мир­но­го тя­го­те­ния вы­ра­зи­те массу и най­ди­те её ве­ли­чи­ну (в килограммах), если и гра­ви­та­ци­он­ная по­сто­ян­ная

2. Упростите вы­ра­же­ние  

8 класс: 

1. На окруж­но­сти с цен­тром O от­ме­че­ны точки A и B так, что Длина мень­шей дуги AB равна 88. Най­ди­те длину боль­шей дуги.

2. Из точки А про­ве­де­ны две ка­са­тель­ные к окруж­но­сти с цен­тром в точке О. Най­ди­те рас­сто­я­ние от точки А до точки О, если угол между ка­са­тель­ны­ми равен 60°, а ра­ди­ус окруж­но­сти равен 8.

3. Радиус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду AC в точке D и пер­пен­ди­ку­ля­рен ей. Най­ди­те длину хорды AC, если BD = 1 см, а ра­ди­ус окружности

Домашнее задание (6, 7 классы)

6 класс:

1. Участникам велогонок необходимо проехать б кругов по окружности радиусом 180 м. Какое расстояние должны проехать спортсмены?

2.На пути в 450 м колесо телеги сделало 150 оборотов. Найдите диаметр колеса.

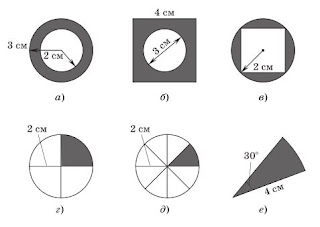
3. Найдите площадь закрашеной части фигуры.

7 класс (алгебра):

1. Найдите зна­че­ние вы­ра­же­ния  при a = 7,7.

2. Упростите вы­ра­же­ние , най­ди­те его зна­че­ние при .

3. Закон Менделеева-Клапейрона можно за­пи­сать в виде PV = νRT, где P — дав­ле­ние (в паскалях), V — объём (в м³), ν — ко­ли­че­ство вещества (в молях), T — тем­пе­ра­ту­ра (в гра­ду­сах Кельвина), а R — уни­вер­саль­ная газовая постоянная, рав­ная 8,31 Дж/(К⋅моль). Поль­зу­ясь этой формулой, най­ди­те давление P (в Паскалях), если T = 250 К, ν = 16,4 моль, V = 8,2 м³.


7 класс (геомептрия):

1. Пря­мые m и n параллельны. Най­ди­те ∠3, если ∠1= 38°, ∠2 = 76°. 

2. На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 72°. Найдите угол CMA. Ответ дайте в градусах.

3. Бис­сек­три­сы углов N и M тре­уголь­ни­ка  MNP  пе­ре­се­ка­ют­ся в точке  A. Най­ди­те  , если  , а  

Информатика

Тренировка 20.1
Остальное